Inhoudsopgave           De Harmonie der Sferen Griekse Muziekale Astronomie

De oudste bronnen voor de ‘Harmonie der Sferen’ zijn Plato’s werken Timaeus en Staat. Uit de getallen die Plato (427-347 v.c.) de Demiurg (δημιουργόσ- lett. ‘handwerksman’, fig. ‘Schepper’ - ‘God’) in de Timaeus (35B) laat gebruiken als onderdeel van de constructie van de kosmos, kan een toonladder worden afgeleid waarin de ideale afstanden tussen de verschillende hemellichamen ‘klinken’. In de Timaeus is echter nog geen sprake van de ‘muziek der sferen’. Dat idee is afkomstig uit een andere bron, namelijk de mythe van Er aan het einde van de Staat. Ik zal beide achtereenvolgens behandelen.

In de dialoog Timaeus laat Plato zijn fictieve personage, de pythagoreeër Timaeus uit Locrië (een plaats in Magna Graecia, de Griekse kolonie in Zuid-Italië), vertellen hoe de Handwerksman (δημιουργόσ) de wereld tot stand bracht. Deze vertelling verloopt ongeveer als volgt.
Omdat de Handwerksman (door Plato ook God, θεός, genoemd) volkomen goed is, en slechts het goede wil, schiep(1) hij één en slechts één volmaakt goed universum (31A-B), als een levend wezen (29E-30C), met een volmaakte vorm, de bol, en een volmaakte beweging, roterend om zijn eigen as; dus cirkelvormig bewegend (33B-34B). Dit levende wezen dat al het leven in zich bevat (33B), bestaat enerzijds uit stof (in de vereniging van de vier elementen, 31B-33B), anderzijds uit geest, de ‘wereld-ziel’.
De wereld-ziel bestaat uit drie elementen, namelijk Bestaan, Gelijkheid en Verschil; deze drie, die gescheiden waren, werden tot een eenheid gebracht.(2) Want de Handwerksman dwong Verschil met kracht tot een band met Gelijkheid (in de wereld-ziel bestaat dus harmonia!) en smeedde deze vervolgens met de hulp van Bestaan tot één geheel (35A). Daarop mat hij op de zo ontstane eenheid een aantal delen af (35B); uit deze verdeling kunnen de intervallen van een toonladder worden afgeleid.

De drieëenheid van Bestaan, Gelijkheid en Verschil (bijvoorbeeld te vergelijken met een stuk platgehamerd metaal), met de daarop afgemeten intervallen, sneed de Handwerksman daarna over de lengte doormidden, en legde de twee helften in de vorm van de letter chi (C), waarna hij de uiteinden naar elkaar boog waardoor twee cirkels ontstonden.
Vervolgens bracht hij beide cirkels in beweging, de beweging van de binnenste cirkel noemde hij ‘beweging van Verschil’ en deze liep diagonaal van rechts naar links, de buitenste (‘beweging van Gelijkheid’) echter horizontaal van links naar rechts (36B-C). De buitenste cirkel liet hij verder met rust, maar de binnenste verdeelde hij in zeven cirkels van ongelijke grootte (36C-D). Op deze wijze construeerde de Handwerksman, of God, de kosmos.
De buitenste cirkel (‘Gelijkheid’) kan gelijk worden gesteld met de hemelequator (de snijcirkel van het vlak door de evenaar van de aarde met de hemelbol) en daarmee aan de sterrenhemel, die inderdaad van links naar rechts, oftewel van Oost naar West beweegt.
De binnenste cirkel (‘Verschil’) kan worden gelijkgesteld met de zodiac (dierenriem), een denkbeeldige gordel van 8 graden aan weerszijden van de ecliptica (de baan die de zon in één jaar aflegt langs de hemelbol, wanneer men de aarde in rust denkt - dus een schijnbare beweging).

afb. 1 ‘Plato’s kosmologie’ uit: David C. Lindberg, The Beginnings of Western Science. Chicago/London, The Univ. Of Chic. Press, 1992.p. 43

De planetenbanen (maar ook die van zon en maan) bevinden zich in de cilin- der die van de zodiac kan worden voorgesteld; de planeten, zon en maan bewegen dus langs de tekens van de dierenriem (de sterrenconstellaties Ram, Stier etc. die zich in de ‘buitenwand’ van deze cilinder bevinden), een gegeven dat niet on- belangrijk in de astrologie schijnt te zijn. De planeten, zon en maan bewegen zich van West naar Oost aan de hemel en bevinden zich in de zeven kleinere cirkels die de Handwerksman van de binnenste cirkel maakte (zie afbeelding 1).(3)

Om nu op de verdeling van de drieëenheid terug te komen (waaruit een toonladder kan worden afgeleid): de Handwerksman nam eerst 1 deel, toen 2 delen, vervolgens 3, 4, 8, 9 en tenslotte 27 delen (35B-C). Deze getallen (1, 2, 3, 4, 8, 9, 27), waarop de orde in de wereld berust, ontnam Plato aan de tetraktys(4); in feite is er sprake van twee tetraktues: 1, 2, 4, 8 en 1, 3, 9, 27. De ene tetraktus bevat de tweede en derde macht van 2, de even getallen; de andere tetraktus dezelfde machten van 3, de oneven getallen.(5)
Ook de verhoudingsgetallen van de eenvoudige consonanten kunnen aan deze getallenrij ontleend worden, en zo kan een toonreeks opgesteld worden waarin tevens de Platonische planetenvolgorde (maan, zon, venus, mercurius, mars, jupiter en saturnus - zie ook de 1e pagina, het systema Platonicum) onder gebracht kan worden; de zeven getallen vormen dan de ideale afstanden tussen de zeven hemellichamen (vijf planeten, zon en maan).(6)

Het grote probleem is echter dat deze toonreeks van vier octaven en een (grote) sext veel groter is dan welk Grieks toonsysteem ook. Cornford citeert echter Theon van Smyrna (ca. 115-140 n.c.) die opmerkte dat Plato met wetenschap bezig is, en niet met praktische muziek.(7) Daarnaast, Von Jan merkt op dat deze getallen de eenvoudigste gehele getallen zijn waarmee de verhoudingen tussen de intervallen samengesteld kunnen worden; breuken zouden de eenvoud en daarmee de symmetrie met de zeven hemellichamen verstoren.(8)

Dit wat betreft de Timaeus.

Een andere plaats(10) waar Plato over de Harmonie der Sferen spreekt is aan het einde van de Staat (Politeia) - boek 13, 614 e.v., - waar hij afsluit met de mythe van Er; deze mythe verloopt ongeveer als volgt.
De Pamphylische heros Er, zoon van Armenius, werd voor dood gevonden op het slagveld. Toen hij ontwaakte, vlak voordat zijn brandstapel aangestoken zou worden, vertelde hij dat hij getuige was geweest van hetgeen de mens na de dood gebeurt: de zielen van de mensen worden geoordeeld voor hun daden op aarde en daarvoor gestraft of beloond. Ook, zo vertelde Er, had hij de spoel van Noodzakelijkheid (Ἀνάγκη, personificatie van het noodlot) gezien (616C).
Deze spoel (als van een spinnewiel) bevindt zich in het midden van de kosmos en is gemaakt van adamant en gekleurd als een regenboog, maar veel helderder en zuiverder. Zij dient als naaf voor een achttal sferen en ligt in de schoot van Ἀνάγκη de buitenste sfeer draait het snelste, de zeven sferen binnen de buitenste echter hebben alle een verschillende snelheid en draaien tegenovergesteld aan de draairichting van de buitenste. De bovenkant van de sferen is afgesneden en alle acht hebben verschillende kleuren.
De pythagoreïsche verhoudingen uit de Timaeus ontbreken, maar er is muziek aanwezig: ‘And the spindle turned on the knees of Necessity, and up above on each of the rims of the circles a Siren stood, borne around in its revolution and uttering one sound, one note, and from all the eight there was the concord of a single harmony.’ (‘... ἐκ πασών δέ ὀκτὠ οὐσῶν μίαν ἁρμνἰαν ξθμφωνεῖν’)(11)
Aan weerszijden van de troon van Ἀνάγκη zitten drie vrouwen, Láchesis, Cloto en Atropos; de drie schikgodinnen. Zij bezingen heden, verleden en toekomst en doen de sferen bewegen. Vervolgens ziet Er hoe de zielen een nieuw bestaan mogen uitkiezen en uit de Lethe drinken om hun oude leven te vergeten; Er mag hieruit niet drinken. Vanwege hun vrijheid om naar eigen believen een bestaan te kiezen zijn de zielen dus zèlf verantwoordelijk voor hun lot op aarde, en niet de Goden (vgl. Odyssee α 31-32).
De kosmologie in de Staat komt hiermee overeen met die in de Timaeus: een achttal sferen die om elkaar wentelen. Verschillend is echter dat niet de planeten, maar de Sirenen(12) voor de Harmonie der Sferen verantwoordelijk zijn; mogelijkerwijs gebeurt dit vanwege het visionaire karakter van de mythe, zo schrijft James Haar: ‘Thus for Plato the universe was designed according to harmonious proportions (Timaeus), and this intellectual harmony could be described in the metaforic language of a dream-vision, as sounding music.’(13)

1. Over de vraag in hoeverre Timaeus’ verhaal op fantasie berust, met andere woorden, welke gedeelten als wetenschap bedoeld zijn en welke als mythe; en over de vraag of de wereld ontstaan is, uit chaos (de oerstof die de Handwerksman naar vorm van de Ideeën ‘kneedde’), of altijd al bestaan heeft en slechts in eeuwigdurende wording is, wordt sinds de oudheid al getwist. Zie Emile de Strycker, Beknopte geschiedenis. pp. 105-106 (terug naar tekst)
2. ‘θάτερον’ wordt door Francis MacDonald Cornford (Plato’s Cosmology. London, Routledge and Keegan Paul, 1956 p. 59 e.v) vertaald als ‘Difference’, door R.G. Bury (Timaeus. Cambridge (Mass.), Harvard Univ. Press, 1989. The Loeb Classical Library. p. 66) echter als ‘Other’. Naar mijn mening drukt ‘Verschil’ beter dan ‘Ander’ de ongelijkheid met ‘Gelijkheid’ uit (‘ταὐτόν’ - lett. ‘hetzelfde’).(terug naar tekst)
3. Zie ook Francis MacDonald Cornford, Plato's Cosmology. p. 73 e.v. (terug naar tekst)
4. De getallen waren voor de pythagoreërs geen abstracta, zoals bij ons, maar zij werden ruimtelijk gepresenteerd, door middel van steentjes die in geometrische figuren werden gelegd. Zo legde men driehoeksgetallen, vierkante getallen en langwerpige getallen.

Het voornaamste driehoeksgetal was de ‘heilige pythagoreïsche tetraktus’ (τετρακτὐς), of de som van de eerste vier getallen (1+2+3+4=10). De geometrische figuur van dit drie hoeksgetal zag er als nevenstaand uit. Behalve dat men uit deze figuur en de daarbij behorende getallen de verhoudingen van de intervallen afleidde, namelijk dubbeloctaaf (4:1), duodecime(3:1), octaaf (2:1), kwint (3:2), en kwart (4:3) - de enige intervallen die als consonant werden beschouwd, - symboliseerde de

tetraktus daarnaast ook andere verbanden in de wereld. Bijvoorbeeld in het menselijk leven de vier leeftijden (kindheid, jeugd, volwassenheid, en ouderdom), of de maatschappij (de mens zelf, dorp, stad, en land). Het driehoeksgetal legde men in de vorm van een gelijkzijdige driehoek en het is aardig te bedenken dat een loodlijn getrokken vanuit een punt naar een basis twee rechthoekige driehoeken oplevert, driehoeken waarop de stelling van Pythagoras (a²+b²=c²) van toepassing is. Ook symboliseerde de τετρακτὐς de vier (wiskundige) dimensies, namelijk 1=punt, 2=lijn, 3=vlak en 4=lichaam, te weten de vijf platonische lichamen, namelijk kubus, tetraeder (piramide), octaeder, isocaeder en dodecaeder (zie Joh. Kepler, afbeelding 1). Deze lichamen gebruikte Plato in de Timaeus (54C-56B) om de materie te verklaren, ook werden zij door Johannes Kepler (ibid.) gebruikt als onderdeel van zijn kosmologie. Zie Emile de Strycker, Beknopte geschiedenis. p. 28; Edward A. Lippman, Musical Thought. p. 16; Francis McDonald Cornford, Plato's Cosmology. p. 70; Leo Spitzer, ‘Classical and Christian Ideas of World Harmony' loc. cit. II, p. 414; of Richard L. Crocker, ‘Pythagorean Mathematics and Music' Journal of Aesthetics and Art Criticism 22 (1963-64): pp. 189-98 en 325-335 (terug naar tekst)
5. Zie hierover verder Francis MacDonald Cornford, Plato’s Cosmology. p. 67; of Hans Schavernoch, Sphären. p. 71 (terug naar tekst)
6. Voor deze volgorde, zie bijvoorbeeld Timaeus 38C-D, waar Timaeus vertelt dat de Handwerksman zeven cirkels maakte van de ‘beweging van Verschil’, de maan in de binnenste cirkel het dichtst bij de aarde plaatste, enzovoorts. Zie ook Carl von Jan, ‘Die Harmonie der Sphären’ loc. cit. p. 18 voor verdere vindplaatsen van deze volgorde bij Plato; maar zie ook Francis MacDonald Cornford, Plato’s Cosmology. p. 105, of Hans Schavernoch, Sphären. p. 52 en 70 (terug naar tekst)
7. Francis MacDonald Cornford, Plato’s Cosmology. p. 67-68 (terug naar tekst)
8. Zie Carl von Jan, ‘Die Harmonie der Sphären’ loc. cit. p. 27 (terug naar tekst)
9. Er bestaat een aantal oplossingen voor deze toonladder, ik heb die van Cornford (op. cit. p. 69) overgenomen, echter met een verschil, Cornford begint op C (vanwege de overzichtelijkheid?), ik begin op A: de laagste toon in het Griekse toonsysteem (de proslambenomenos). Voor een bibliografie van deze verschillende oplossingen zie Hans Schavernoch, Spären. p. 233 (noot 203). Niet door Schavernoch genoemd is Jacques Handschin, ‘The Timaeus Scale’ Musica Disciplina 4 (1950): pp. 3-42. Wat betreft de afstanden: de maan bevindt zich het dichst bij de aarde (dus: 1), saturnus het verst weg (dus: 27). (terug naar tekst)
10. Ook bijvoorbeeld in Plato’s Phaedrus vind men verwijzingen naar een kosmologie. Zie bijvoorbeeld Kathi Meyer-Baer, Music of the Spheres and the Dance of Death. p. 11 e.v. of Heinrich Hüschen, ‘Harmonie’ MGG 5. kols. 1601-1602 (terug naar tekst
11. Plato, Politeia. 617 B. Vert. Paul Shory, The Republic. Cambridge (Mass.), Harvard U.P., 1969-70. 2 dl. (The Loeb Classical Library). II, p. 502-505 (terug naar tekst)
12. Dat de Sirenen, die van oorsprong de duistere kant van de muziek vertegenwoordigen (zie bijv. de Odyssee m 135 e.v.), hier deze rol spelen is opmerkelijk. Hans Schavernoch (Sphären. p. 65-66) merkt hierover op dat de Sirenen als tegenhangers van de negen aardse muzen fungeren: waar de muzen de mens op aarde met muziek (en andere kunsten) steunen en begeleiden, zo doen de Sirenen dat na de dood. Over de muzen en hun rol in de Harmonie der Sferen, zie Hans Schavernoch, Sphären. pp. 84-85; Marie T. d’Alverny, ‘Les muses et les sphères célestes’ in: C. Henderson (ed.), Classical, Medieval and Renaissance Studies in Honour of B.L. Ullman. Rome, 1964. 2. pp. 7-19; Pierre Boyancé, ‘Les muses et de l’harmonie des sphères’ Melanges dédiés à la memoire de Félix Grat. Paris, Pequeur-Grat, 1946-1949. (2 dl.). II, p. 3 e.v., en van dezelfde schrijver: Le culte des muses. Paris, 1937; of Ernst R. Curtius, Europäische Literatur und lateinisches Mittelalter. Bern, A. Francke Verlag, 1948. pp. 233-250 (terug naar tekst)
13. James Haar, ‘Pythagorean Harmony of the Universe.’ DHI 4. p. 39 (terug naar tekst)
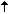