Inhoudsopgave           De modi De vier stemmen: diskant, alt, tenor en bas

In het zevende hoofdstuk beschrijft Kepler hoe meerstemmigheid kan worden afgeleid uit de schijnbare snelheden, hierbij gaat hij uit van de gegevens uit de rechterkolom van tabel 1 (saturnus A:P verhoudt zich als 4:5, etc.). Dit hoofdstuk luidt hij als volgt in:

‘Nu is nodig, Urania, een groot geluid, terwijl ik op de harmonische ladder van de hemelse bewegingen naar grotere hoogten opklim, daarheen waar het ware, verborgen origineel van de wereldbouw bewaard wordt.’ (Nunc opus, Vranie, sonitu majore: dum per scalam Harmonicam coelestium motuum, ad altiora conscendo; qua genuinus Archetypus fabricae Mundanae reconditus asservatur.(1)).

De meerstemmige muziek, zo vervolgt Kepler, die in de oudheid onbekend was, is de waarachtige spiegel van de wereld: in haar openbaren zich de geheimen van de Schepping aan de geesten van de mensen.(2) Meerstemmigheid in de Harmonie der Sferen is Keplers grote vernieuwing; deze meerstemmigheid kan voorkomen als twee-, drie-, vier-, vijf- of zesstemmigheid, dus tussen twee tot zes planeten. In de hemel klinken niet meer dan zes stemmen, want de maan heeft geen eigen stem, maar zingt met de aarde mee. (Verum heus vos, in coelo plures quam sex non concordant. Nam Luna seorsim suam Monodiam cantillat, Terris ut cunis affidens.(3)).
Kepler begint met de opmerking dat hij de harmonische verhoudingen tussen snelheden van naburige planeten reeds getoond heeft (tabel 1, linkerkolom). Meer bijzonder echter, zo vervolgt hij, is de harmonie die ontstaat wanneer twee planeten tegelijkertijd in hun apsis staan (de apsis wordt gedefinieerd als elk der uiteinden van de lijn die de twee uiterste punten van de grote as van een ellips met elkaar verbindt, deze uiterste punten komen natuurlijk overeen met aphelium en perihelium).(4) Deze gebeurtenis is zeer zeldzaam, zeker wat betreft de buitenste planeten (in Keplers tijd jupiter en saturnus), die immers het langzaamst bewegen. Kepler geeft jupiter en saturnus dan ook als voorbeeld voor de zeldzaamheid van deze gebeurtenis.
In de tussentijd echter kunnen de planeten ook harmonieën produceren. Bijvoorbeeld (zie tabel 3): saturnus beweegt van G naar B, jupiter van B naar d (N.B. gezien de reductie in tabel 2 in werkelijkheid een octaaf hoger!, vandaar intervallen als een decime etc.), buiten de apsis-intervallen (saturnus A en jupiter P: G-d, een duodecime; ten tweede: saturnus P en jupiter A: B-B, een octaaf) kunnen dus bijvoorbeeld ook een grote of kleine decime (G-B, B-d, A-c) ontstaan, of een undecime (G-c, A-d), en, gezien de continue (glissando) beweging, alles daartussenin.

Tweestemmigheid komt zo het meest voor, temeer daar de andere planeten (mercurius, venus, aarde en mars) sneller bewegen, en dus vaker harmonische verhoudingen samenstellen. Dit laatste is zeker het geval wat betreft mercurius, vanwege diens grote snelheid, en dus grote ambitus, kan deze bijna altijd in een harmonie worden ingepast.(5)

Ook driestemmige harmonieën komen redelijk vaak voor, hoewel minder vaak dan tweestemmige. Het lijkt erop, zo zegt Kepler, dat driestemmige harmonieën vanwege de relatief grote snelheid van mars, aarde en mercurius tussen deze drie vaker voorkomen. Maar vooral venus moet, vanwege haar geringe beweeglijkheid, geduldig wachten tot haar toon mee kan klinken met de anderen.(6)

Harmonieën tussen vier planeten hebben echter al honderden jaren nodig om te ontstaan, harmonieën tussen vijf planeten meer dan myriaden van jaren; een Eeuwigheid scheidt de harmonieën van zes planeten.(7)

Kepler vermoedt dat er slechts eenmaal een harmonie tussen zes planeten zich heeft voorgedaan, namelijk bij de schepping, aan het begin van de tijd en hij weet niet of er ooit twee zulke momenten zullen zijn (misschien dat Kepler zich voorstelde dat op de jongste dag in de hemelen voor de tweede en laatste maal een harmonieus akkoord van zes stemmen, zes planeten, zou klinken, waarna de hemelen voor eeuwig zouden verstommen).(8)
Wanneer er nu een zestemmige harmonie in de hemel te vinden is, dan is deze volgens Kepler de constellatie van de planeten aan het begin van de schepping (men zou dus, als deze harmonie aanwijsbaar is, in de tijd terug kijken naar het ‘begin’). ‘Te vragen is derhalve’, zo vervolgt Kepler, ‘òf, en op hoeveel manieren de bewegingen van de planeten in één gemeenschappelijke harmonie kunnen worden samengebracht.’ (Quaerendum igitur, an et quot omnino formis redigantur omnium sex planetarum motus in unam communem harmoniam?(9)).

Het uitgangspunt bij de samenstelling van deze zesstemmige harmonieën zijn de bewegingen van aarde en venus, omdat deze vanwege hun geringe beweging maar twee consonanten met elkaar kunnen vormen. (Methodus inquisitionis haec est, ut incipiamus a Terra et Venere; quia hi duo faciunt consonantias non plures duabus, et (quod huius rei causam continet) per intensiones motuum brevissimas.(10)). Als nu voor de aarde weer de ‘g’ wordt genomen en voor venus een ‘e’ respectievelijk een ‘es’, dan weet Kepler hiermee twee ‘sceleta Harmoniarum’(11) samen te stellen (best te vertalen als ‘harmonisch raamwerk’, hoewel ‘akkoord’ alleszins ook mogelijk is): een durus-raamwerk, gebaseerd op het interval g-e (de grote sext), en een mollis-raamwerk, gebaseerd op het interval g-es (de kleine sext). Er kunnen meerdere noten uit een planeetinterval in een raamwerk gepast worden wanneer deze consoneren. Een ‘sceletum’ is dus een verzameling mogelijke akkoorden, waarvan er echter maar een op een bepaald moment ‘klinkt’.
Kepler hanteert twee stemmingen (‘tensiones’): een lage stemming en een hoge. De reden hiervoor is dat de schijnbare snelheid van een planeet continu varieert (dichterbij de zon sneller, omgekeerd wanneer verder weg). Als alle tonen uit een raamwerk binnen hun eigen maximale (schijnbare) snelheid blijven dan kunnen de tonen (die met een bepaalde schijnbare snelheid corresponderen) binnen een bepaalde stemming verhoogd of verlaagd worden, om zo de verschuivingen in snelheid op te vangen.

In het durus-raamwerk worden de grondwaarden bepaald door aarde A (57’3’’) voor de laagste stemming en door venus P (97’37’’) voor de hoogste stemming. Een voorbeeld: uit venus P (97’37’’) ontstaat in de hoge stemming jupiter A als volgt: 97’3’’ gedeeld door vier octaven en een kwart (van e5 naar b) = 97’37’’ : 16 : 4/3 = 4’34’’, hetgeen de waarde is van jupiter A in figuur 1 (zie onder, of afbeelding 35a voor het origineel uit HM.), en binnen de marge jupiter A-P (4’30’’ - 5’30’’) valt. De overige waarden worden evenzo afgeleid.
Door deze wijze van berekenen ontstaan er ander tonen (corresponderend met andere schijnbare snelheden) voor de verschillende planeten; nogmaals, de enige eis die Kepler stelt is dat de nieuwe waarden binnen de maximale waarden voor A en P van de verschillende planeten vallen.(12) Gevolg hiervan is bijvoorbeeld dat mercurius’ e7 in de hoogste stemming is weggevallen: de hoogste stemming zou zijn 390’28’’ (2 x 195’14’’ van het octaaf e6 daaronder), dit is meer dan de maximale waarde van 384’0’’.
Er zijn echter wel enige ‘onzuiverheden’ in figuur 1. Kepler gaat namelijk niet helemaal nauwkeurig te werk: de waarde van mars P (38’2’’) in figuur 1 (lage stemming, tweede akkoord) is een seconde groter dan toegestaan; een seconde meer dan 38’1’’ (zie tabel 1). Deze afwijking wordt gecompenseerd door het feit dat mars P nog een toon heeft, hierdoor blijft de universele harmonie aanwezig, zelfs wanneer men zeer strikt zou zijn en mars P c4 zou weglaten (wanneer een planeet meerdere tonen heeft is het verlies van een minder erg). Jupiter echter heeft in de lage stemming (figuur 1, eerste akkoord) geen toon, hierdoor is er in feite geen sprake meer van ‘universele harmonie’ (er ontbreekt een toon!), hetgeen blijkbaar geen reden was voor Kepler zijn berekeningen te herzien.(13)
Dezelfde berekeningen als bovenstaande heeft Kepler gebruikt voor het tweede ‘universele akkoord’, maar nu zo, dat er een ‘c’ in plaats van een ‘b’ verschijnt. De reden voor deze tweede berekening is dat Kepler probeert zo veel mogelijk extreme bewegingen in de akkoorden onder te brengen, want hoe meer extreme bewegingen, hoe ‘universeler’ het akkoord, en hoe universeler het akkoord, hoe dichterbij Kepler aan het moment van de schepping raakt, en daarmee aan zijn uiteindelijke doel: het onthullen van Gods bouwplan voor deze wereld.
Figuur 1 toont deze twee universele akkoorden en de extreme bewegingen die ermee worden uitgedrukt (zie ook afbeelding 28a voor het origineel uit HM.):

Het eerste akkoord (links) in figuur 1 bestaat uit de tertsligging van een e-klein akkoord (in totaal 4 x 2 x 2 = 16 combinaties); het tweede akkoord (rechts) uit een kwartsextligging(15) van een C-groot akkoord (in totaal 4 x 2 = 8 combinaties). Overigens, de vele lijnen boven de onderste notenbalk (saturnus, met f-sleutel) dienen alle als hulp-lijnen opgevat te worden.

Evenzo construeert Kepler twee akkoorden met het mollis-raamwerk: een tertsligging van en Es-groot akkoord en en kwartsextligging van een c-klein akkoord, de vele mollen in deze figuur (2, zie onder, of afbeelding 35b voor het origineel uit HM.) duiden slechts de plaats van de bes aan, niet zozeer een actuele verlaging.
Het verschil met figuur 1 is dat Kepler nu alleen uitgaat van de extremen van venus (P: 97’37’’ en A: 94’50’’) en aan de hand van alleen deze de overige tonen berekent. (bijvoorbeeld: aarde A is nu 59’16’’ in plaats van 57’3’’, maar zie ook de snellere beweging van saturnus; deze nieuwe bewegingen bevinden zich echter wel binnen hun maxima). Boven deze figuur (2), eerste akkoord (e-klein) staat in de druk uit 1619 ‘ut h concordet’, dit nu is onjuist, er had ‘ut b concordet’ moeten staan, want niet de b, maar de bes klinkt (zie afbeelding 28b).
Ook hier wordt een onzuiverheid aangetroffen: mercurius’ c6 ligt beneden de maximaal toegestane waarde (162’43’’ in plaats van 164’0’’). Wederom wordt dit gemotiveerd uit het feit dat dat Kepler zo veel bewegingen als maar mogelijk zijn in zijn universele akkoorden onder wil brengen.

Uit deze ‘universele harmonieën’ concludeert Kepler dat:

‘Derhalve bewijst de astronomische ervaring dat er universele harmonieën van alle bewegingen kunnen ontstaan, en wel in twee geslachten durus en mollis en in beide geslachten van tweeërlei vorm, of (als dit toegestaan is) van een tweevoudige toonsoort; in elk van de vier gevallen met een zekere stemmingsomvang en ook met een zekere verscheidenheid van de afzonderlijke harmonieën van saturnus, mars, en mercurius, en elk van deze met de anderen. De ervaring bewijst tevens dat dit niet alleen gebeurt met de tussenliggende bewegingen, maar geheel en al met alle extreme bewegingen, behalve die van het aphelium van mars en het perihelium van jupiter.’ (Testatur igitur experientia Astronomica, posse contingere universales omnium motuum Harmonias, easque duorum generum, Duri et Mollis; et in utroque genere, formae seu (si ita licet) Toni duplicis; et in uno quolibet quatuor casuum, cum aliqua tensionis latitudine, et cum aliqua etiam varietate particularium Harmoniarum Saturni, Martis et Mercurii, cujusque cum caeteris: nec id praestari solis motibus intermediis, sed omnino extremis omnibus, praeterquam aphelio Martis et perihelio Jovis ....(17)).

De laatste opmerking is de belangrijkste: de getoonde harmonieën berusten niet op de oneindige variëteit van de tussenliggende bewegingen, maar zij berusten op de extreme bewegingen, uitgedrukt door aphelium en perihelium.
Zo kan Kepler in bovenstaande vier akkoorden bijna alle extreme hoeksnelheden een plaats bieden, behalve aan jupiter P en mars A; want jupiter P zou een ‘d’ en mars ‘a’ een fis moeten krijgen, maar deze noten klinken niet goed samen met de ‘e’ van venus. Kepler voert de volgende bijzonder reden aan voor deze dissonantie: als venus een grotere vrijheid zou hebben (dan de eeuwigdurende beweging tussen e en dis) dan konden mars en jupiter ingepast worden, maar haar huwelijk met haar man aarde laat haar echter die vrijheid niet, zij is gebonden.(18)
Om nu toch alle extremen onder te brengen, hoewel helaas niet niet in een akkoord, stelt Kepler een tweede reeks akkoorden op, maar nu wordt venus weggelaten. Op deze manier kan Kepler, echter wel vijfstemmig, de ‘d’ van jupiter P kwijt; en door nog een stem te laten vallen (de aarde, de tweede probleemveroorzaker) kan Kepler ook de ‘fis’ van mars A een plaats bieden.
Kepler verkrijgt op deze wijze een vijfstemmig G-majeur en g-mineur akkoord (terts- en grondligging) door venus weg te laten; en een vierstemmig b-mineur akkoord alswel een D-majeur akkoord (beide in gronligging) door zowel venus als de aarde weg te laten. Waarom Kepler deze laatste twee akkoorden zonder stemming weergeeft is onbekend.(19) In afbeelding 28b en c zijn deze twee akkoorden te vinden (N.B. Kepler laat venus in het vijfstemmige akkoord niet weg, maar schrijft ‘venus hindert hier’ - venus hic obstrepit -, en diens noot e5 is ter onderstreping daarvan zwart gemaakt).
Uiteindelijk weet Kepler dan alle twaalf extreme hoeksnelheden in acht grote akkoorden te laten klinken (akkoorden van wel zeven octaven!), jammer genoeg niet in een groot akkoord; want om jupiter plaats te bieden moest venus verdwijnen en voor mars verdween de aarde, juist die planeten moeten verdwijnen waarvan de noten de basis vormen voor Keplers durus- en mollis-raamwerken.

‘Derhalve zijn de bewegingen van de hemelen niets anders dan een voortdurende samenklank (geestelijk, niet klinkend(20)), een samenklank die zich door dissonante spanningen beweegt, zoals door zekere syncopen of cadensen (door welke de mensen dergelijke natuurlijke dissonanten imiteren), naar vaste en voorgeschreven zesdelinge (of zesstemmige) clausulen. Door deze merken articuleert en onderscheidt zij de onmetelijkheid van de Tijd, zodat het niet meer verwonderlijk is dat de kunst van het meestemmig zingen, die onbekend was aan de ouden, door de mens, de aap van zijn Schepper, ontdekt is. Zo kon de mens namelijk de ononderbrokenheid van de Wereldtijd in een kort deel van een uur spelen, door middel van een kunstvolle symphonie van meerdere stemmen, en tot op zekere hoogte het welgevallen van God de schepper in diens werken proeven, in het allerzoetste gevoel van genoegen dat de mens uit deze muziek, de nabootster van God, ontvangt.’ (Nihil igitur aliud sunt motus coelorum, quam perennis quidam concentus (rationalis non vocalis) per dissonantes tensiones, veluti quasdam Syncopationes vel Cadentias (quibus homines imitantur istas dissonantias naturales) tendens in certas et praescriptas clausulas, singulas sex terminorum (veluti Vocem) iisque Notis immensitatem Temporis insigniens et distinguens; ut mirum amplius non sit, tandem inventam esse ab Homine, Creatoris sui Simia, rationem canendi per concentum, ignotam veteribus; ut scilicet totius Temporis mundani perpetuitatem in brevi aliqua Horae parte, per artificiosam plurium vocum symphoniam luderet, Deique Opificis complacentiam in operibus suis, suavissimo sensu voluptatis, ex hac Dei imitatrice Musica perceptae, quadamtenus degustaret.(21)).

Hier eindigt hoofdstuk zeven, het volgende hoofdstuk (acht) is de laatste halteplaats, vòòr Kepler in hoofdstuk negen van start gaat met het bewijs van wat vooralsnog slechts hypothesen zijn.

afb. 28a ‘Zesstemmig planeet-accoord, durus geslacht', HM V, p. 209

afb. 28a ‘Zesstemmig planeet-accoord, mollis geslacht', HM V, p. 210

afb. 28c ‘Vijfstemmig planeet-accoord' HM V, p. 211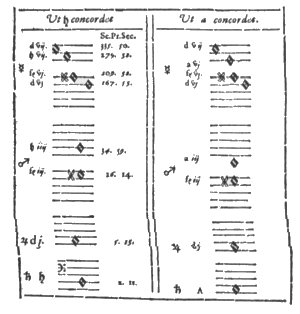

afb. 28d ‘Vierstemmig planeet-accoord', HM V, p. 212

1. HM. V, p. 207-208 (310) (terug naar tekst)
2. Ibid., p. 208 (310) (terug naar tekst)
 3Ibid. Dit citaat is afkomstig uit een margine op deze pagina, waar Kepler tevens de componisten van zij tijd oproept een zesstemming motet te schrijven voor deze ‘lofzang’ (‘pro hoc elegio’, waarschijnlijk bedoelt Kepler hiermee dat zijn gehele Harmonices mundi als één lofzang op de volmaaktheid van de Schepper gezien kan worden). Opdat componisten niet meer of minder stemmen zouden gebruiken vermeldt Kepler nadrukkelijk dat er zes stemmen zijn, hij belooft vervolgens over die zesstemmigheid te waken en merkt daarna op dat degeen die het best in deze compositie slaagt, hem zal de muze Clio een bloemenhulde brengen, en Urania zal hem venus tot bruid geven! (terug naar tekst)
4. Bruce Stephenson (Heavens. p. 171) merkt op dat de zeldzaamheid natuurlijk afhangt van hoe precies men de momenten aphelium en perihelium definieert. Omdat de planeetsnelheden slechts langzaam veranderen rond de apsiden kan Kepler uitgaan van een bepaalde periode in plaats van enkel het precieze apsis-moment. (terug naar tekst)
5. HM. V, p. 208 (311); maar zie ook Bruce Stephenson, Heavens. p. 171 e.v., of Daniel P. Walker, ‘Kepler’s Celestial Music’ loc. cit. p. 248 (terug naar tekst)
6. HM. V, p. 208 (311) (terug naar tekst)
7. Ibid. (terug naar tekst)
8. Ibid. Overigens, de gedachte dat Kepler zich een tweede zesstemmige harmonie op de Jongste Dag zou voorstellen, is niet van mij, maar wordt geuit door Daniel P. Walker (‘Kepler’s Celestial Music’ loc. cit. p. 249). Ik vond dit vermoeden plausibel genoeg om te vermelden. (terug naar tekst)
9. HM. V, p. 209 (311) (terug naar tekst)
10. Ibid. p. 209 (312). Toch is dit niet geheel correct: aarde en venus vormen de consonanten g-e en g-es, maar ook de kleine sext as-e en de kwint as-es, intervallen die Kepler niet gebruikt. Daniel P. Walker merkt hierover enkel op (‘Kepler’s Celestial Music’ loc. cit. p. 249): ‘I do not know why Kepler does not use the possibility ‘as-es’ [curs. van mij, Walker geeft hier notenbalk met noten]. Michael Dickreiter daarentegen (Musiktheoretiker. p. 108 e.v.) besteedt hier meer aandacht aan, hij merkt bijvoorbeeld op dat Kepler in zijn behandeling van de planeet-akkoorden nergens de ‘as’ van de aarde betrekt, ook wijst Dickreiter erop dat de gis (as) in Keplers toonladder niet uit een van de harmonische delingen ontstaat (zie boek III). Je zou dus kunnen zeggen dat de gis (as) niet waardig genoeg is om in de harmonische speculaties over het hemelruim betrokken te worden. (terug naar tekst)
11. HM. V, p. 209 (312) (terug naar tekst)
12. Ibid., p. 209 (312) (terug naar tekst)
13. Bruce Stephenson (Heavens. p. 177) wijst erop dat deze omissie mogelijk is ontstaan toen Harmonices mundi al gezet was bij de drukker en de fout pas daar werd ontdekt. De enige oplossing was toen de toon voor jupiter in de lage stemming maar weg te laten, hoewel het opschrift duidelijk ‘Harmoniae Planetarum omnium’ - alle planeten - vermeldt. Want, zo merkt Stephenson op, Kepler had ook andere, wel kloppende, berekeningen kunnen maken. (terug naar tekst)
14. Naar: HM. V, p. 209 (312) (terug naar tekst)
15. Het is in feite opmerkelijk dat sommige van Keplers universele harmonieën uit akkoorden bestaan die volgens de muziektheorie uit Keplers tijd als dissonant werden beschouwd. Daniel P. Walker (‘Kepler’Celestial Music’ loc. cit. p. 249) merkt hierover op dat de reden hiervoor misschien is geweest dat Kepler uitging van zijn gehoor: een kwartsextakkoord klinkt beslist niet dissonant, slechts theoretisch beschouwde men het als dissonant. (terug naar tekst)
16. Naar: HM. V, p. 210 (313) (terug naar tekst)
17. HM. V, p. 210 (311) (terug naar tekst)
18. Ibid.: ‘[...] quia cum ille [mars] obtineat fis, hic [jupiter] d, Venus obtinens die vel e perpetuo, non fert illos suos vincinos dissonos in harmonia universali, quod faceret sin acta fuisset spacium excendendi ex e vel dis. Hoc impedimenti habet coniugium hoc Telluris et Veneris, ceu maris et feminae [...].’ (terug naar tekst)
19. Kepler schrijft (HM.p. 213/314): ‘Quator vero Planetarum, Saturni, Jovis, Martis, Mercurii, potest et haec esse Harmonia [afbeelding 35d], in quia sit etiam aphelius Martis, sed est sine [ten]sionis.’ (Het eerste gedeelte ten- van tensio is hier weggevallen). Bruce Stephenson (Heavens. p. 183) merkt hierover op: ‘Kepler says that these four-planet harmonies are without latitude of tension, but I do not understand why.’ Kepler had volgens Stephenson beslist wel een stemming kunnen geven, want er is een zekere speelruimte (zo had saturnus bijvoorbeeld ‘versneld’ kunnen worden tot 2’15’’). Om de een of andere reden heeft Kepler dit niet gedaan. (terug naar tekst)
20. Ook op andere plaatsen klinkt Keplers verwerping van de mogelijkheid dat er reële klanken in het hemelruim zouden zijn, bijvoorbeeld: ‘Nu bestaan er in de hemel geen geluiden, noch is de beweging zo onstuimig; dat uit de wrijving van de hemellucht gezoem wordt opgewekt.’ (Iam soni in coeli nulli existunt, nec tam turbulentus est motus; ut ex attritu aurae coelestis eliciatur stridor. HM. V, p. 197/300). Elders haalt Kepler Cicero’s ‘tantus et tam dulcis sonus’ aan, het zoete geluid dat zou ontstaan uit de snelbewegende hemellichamen en Kepler wijst ook op de redenen die Aristoteles aanvoerde waarom dat geluid op aarde onhoorbaar is (HM. IV, p. 106/200). Maar Kepler spreekt over dit alles in een afwijzende toon, zo klint het op (V) p. 178 (279) over Ptolemaeus’ astronomische kennis ‘dat hij [Ptolemaeus] de indruk lijkt te maken eerder met Cicero’s Scipio een lieflijke pythagoreïsche droom voor te dragen, dan filosofische kennis te bevorderen.’ (..., ut qui cum Scipione Ciceroniano potius suave quoddam somnium Pythagoricum recitasse, quam philosophiam adjuvisse videretur.). Maar zie bijv. ook (V) p. 247 (355). (terug naar tekst)
21. HM. V, p. 212 (315)